Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used Truly obscure identities These are just here forThe sure way also stated that, uh, the rest of the trigonometry identities are just receptacles off the 1st 3 Right? Trigonometric Identities The distances or heights can be calculated using mathematical techniques that fall under the category of 'trigonometry'The word 'trigonometry' comes from the Greek words 'tri' (meaning three), 'gon' (meaning sides), and 'metron' (meaning measure) (meaning measure)

Summary Of Trigonometric Identities
Trigonometric identities tangent
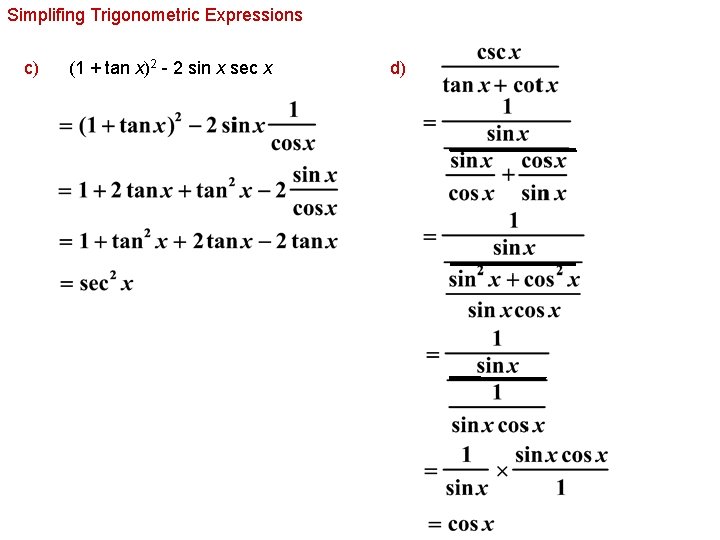
Trigonometric identities tangent-Tangent and cotangent identities Pythagorean identities Sum and difference formulas Doubleangle formulas Halfangle formulas Products as sums Sums as products A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In algebra, for example, we have this identity (x 5)(x − 5) = x 2In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometric




Chapter 7 Trigonometric Identities And Equations Jami Wang
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice;Remember said that So, uh, now you see, this becomes a right triangle, right?Section 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,
Proving Trigonometric Identities To prove an equation is an identity, it requires the knowledge of the existing trigonometric identities For this problem, were going to need the followingSome Useful Trigonometric Identities An identity is an equation whose left and right sides when defined are always equal regardless of the values of the variables the two sides contain Some very useful trigonometric identities are shown below The Pythagorean Identities $$\begin{array}{c} \cos^2 \theta \sin^2 \theta = 1\\ 1 \tan^2 \theta = \sec^2 \theta\\ 1 \cot^2To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x The preceding three examples verify three formulas known as the reduction
Trigonometry 2 expressions and identities AS Level Understand and use tanθ=sinθ/cosθ Understand and use sin^2θcos^2θ = 1 Solve simple trigonometric equations in a given interval, including quadratic equations in sin, cos and tan and equations involving multiples ofDifferentiation of Trigonometric Functions It is possible to find the derivative of trigonometric functions Here is a list of the derivatives that you need to know d (sin x) = cos x dx d (cos x) = –sin x dx d (sec x) = sec x tan x dxTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1



While You Wait Trigonometric Identities And Equations Section



Biomath Trigonometric Functions
Integrals requiring the use of trigonometric identities 2 3 Integrals involving products of sines and cosines 3 4 Integrals which make use of a trigonometric substitution 5 wwwmathcentreacuk 1 c mathcentre 09 1 Introduction By now you should be well aware of the important results that Z coskxdx = 1 k sinkxc Z sinkxdx = − 1 k coskx c However, a little more care is needed when we0 Some common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x = 3 sin x –A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an application is likely to encounter some of these identities Prerequisites Before starting this
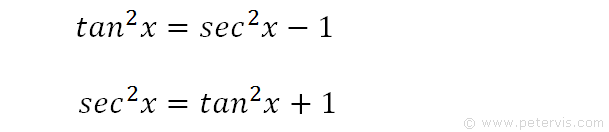



Integrate Sec 2x Method 1



2
Trigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is sin 2 θ cos 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identitiesIt was a right triangle and subtle body We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples Example 1 Prove the following trigonometric




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
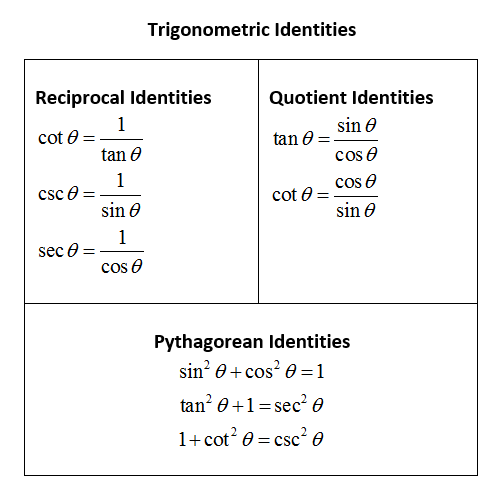
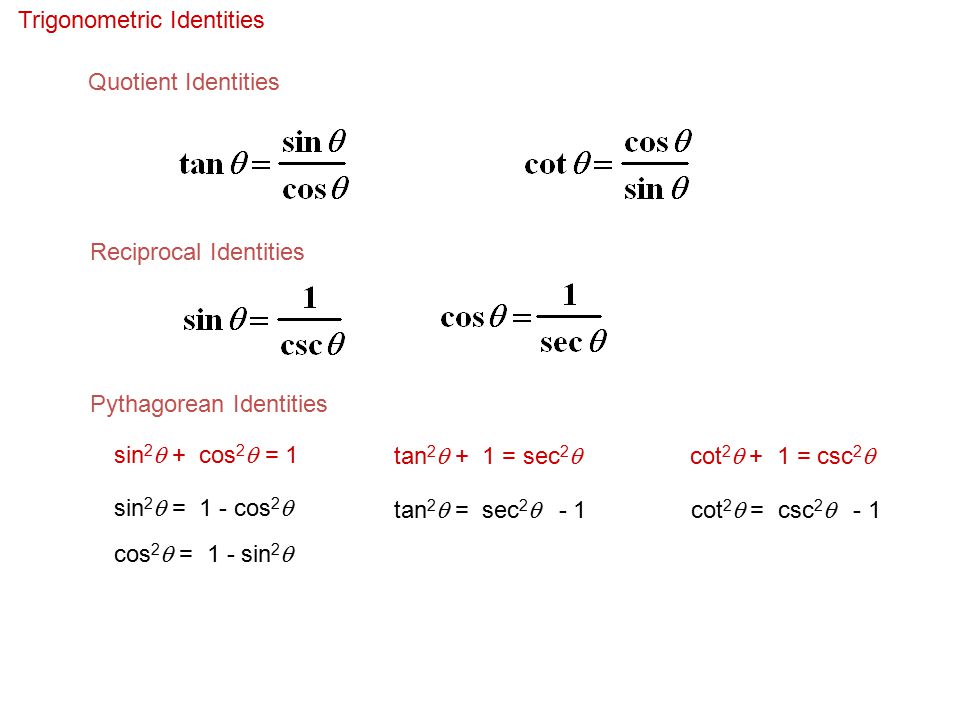
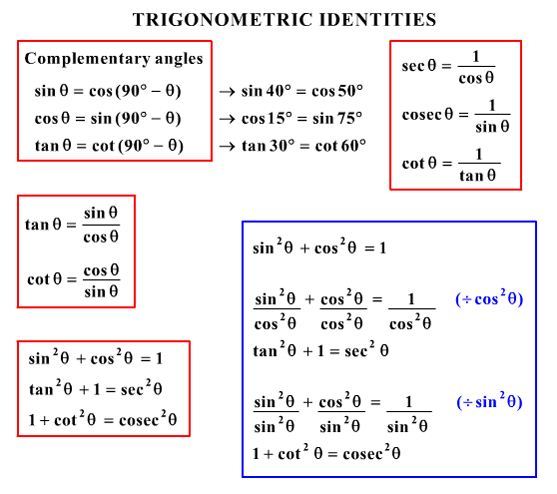
Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu sec(ˇ 2 u) = cscuDefinition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




Chapter 7 Trigonometric Identities And Equations Jami Wang
Trigonometric Identities ( thing) by Rancid_Pickle Mon at Here are sixteen Trigonometric Identities SIN = Sine COS = Cosine TAN = Tangent CSC = CoSecant SEC = Secant COT = CoTangent #1 1 SIN Θ = CSC Θ #2 1 COS Θ = SEC Θ #3 SIN Θ TAN Θ = COS Θ #4 COS Θ 1 COT Θ = = SIN Θ TAN Θ #5 1So it's Xun that in the last year, tutorials before this one has shown that second of his one over co sign a theater, right?1 sin2 x 795 Trigonometric Identities and Equations IC ^ 6 c i1 1 x y CHAPTER OUTLINE 111 Introduction to Identities 112 Proving Identities 113 Sum and Difference Formulas 114 DoubleAngle and HalfAngle Formulas 115 Solving Trigonometric Equations 410_11_p_7956 6 PM Page 795 In this section, we will turn our attention to identities In algebra,




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Trigonometric Identities And Examples With Worksheets
The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radiansTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1Basic Identities 17 sin2 xcos2 x= 1 18 tan2 x1 = 1 cos2 x 19 cot2 x1 = 1 sin2 x Sum and Di erence Formulas 1 wwwmathportalorg sin( ) = sin cos sin cos 21 sin( ) = sin cos sin cos 22 cos( ) = cos cos sin cos 23 cos( ) = cos cos sin cos 24 tan( ) = tan tan 1 tan tan 25 tan( ) = tan tan 1tan tan Double Angle and Half Angle Formulas 26 sin(2 ) = 2 sin cos 27




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
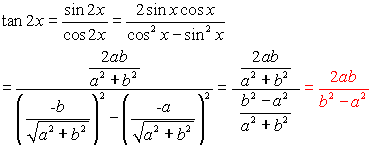



Six Trigonometric Functions Mathbitsnotebook Ccss Math
Notebook Groups Cheat Sheets Sign In; Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead oneIntegral of tan^2(x) How to integrate it step by step!👋 Follow @integralsforyou on Instagram for a daily integral 😉📸 @integralsforyou https//wwwinstag



Solving Trigonometric Equations With Identities Algebra And Trigonometry
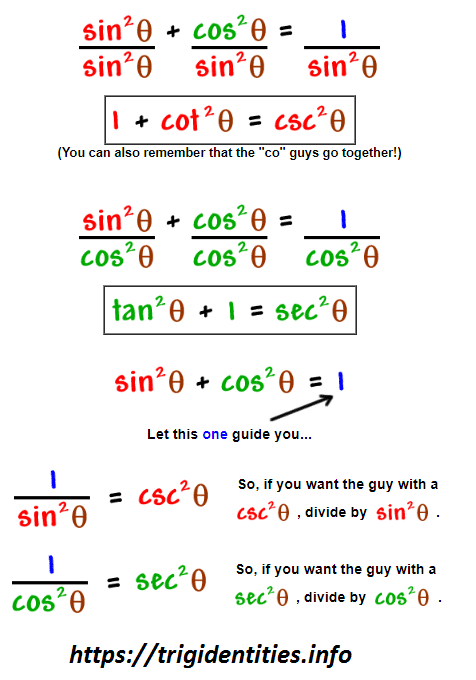



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities
Although these two functions look quite different from one another, they are in fact the same function This means that, for all values of x, This last expression is an identity, and identities are one of the topics we will study in this chapter cos2 x 1 4 sin x 1 2 sin x y cos2 x and y 1 sin4 x 1 sin2 x 795 Trigonometric Identities andTrigonometric identities are equalities62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Quotient identity Quotient identity Complete the table without using a calculator,Account Details Login Options Account Management




Trigonometric Identities A Plus Topper



3
The key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified to (a/c) 2 (b/c) 2 = 1 Now, a/c is OppositeThe "big three" trigonometric identities are sin2 tcos2 t = 1 (1) sin(AB) = sinAcosB cosAsinB (2) cos(AB) = cosAcosB −sinAsinB (3) Using these we can derive many other identities Even if we commit the other useful identities to memory, these three will help be sure that our signs are correct, etc 2 Two more easy identities From equation (1) we can generate two more identitiesThe Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download
Trigonometric functions can have several solutions Sine, cosine and tangent all have different positive or negative values depending on what quadrant they are inA trigonometric equation is an equation that involves a trigonometric function or functions When we solve a trigonometric equation we find a value for the trigonometric function and then find the angle or angles that correspond to that particular trigonometric function 2 Some important identities derived from a rightangled triangleList of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) and cos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ and cos θ The tangent (tan) of an angle is the ratio of the sine to the cosine Finally, the
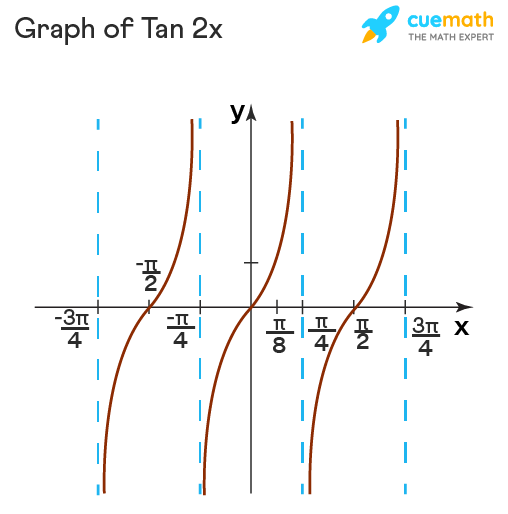



Tan 2x Formula What Is Tan 2x Formula Examples




Worksheet On Trigonometric Identities Establishing Identities Hints
Proving the trigonometric identity $(\tan{^2x}1)(\cos{^2(x)}1)=\tan{^2x}$ has been quite the challenge I have so far attempted using simply the basic trigonometric identities based on the Pythagorean Theorem I am unsure if these basic identities are unsuitable for the situation or if I am not looking at the right angle to tackle this problem trigonometry ShareFollowing table gives the double angle identities which can be used while solving the equations You can also have #sin 2theta, cos 2theta# expressed in terms of #tan theta # as under #sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)#Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos Compoundangle formulae cos(A B) = cosAcosB sinAsinB (4) cos(A B) = cosAcosB sinAsinB (5) sin(A B) = sinAcosB cosAsinB (6) sin(A B) = sinAcosB cosAsinB (7) tan(A B) = tanA tanB 1 tanAtanB (8) tan(A B) = tanA tanB 1
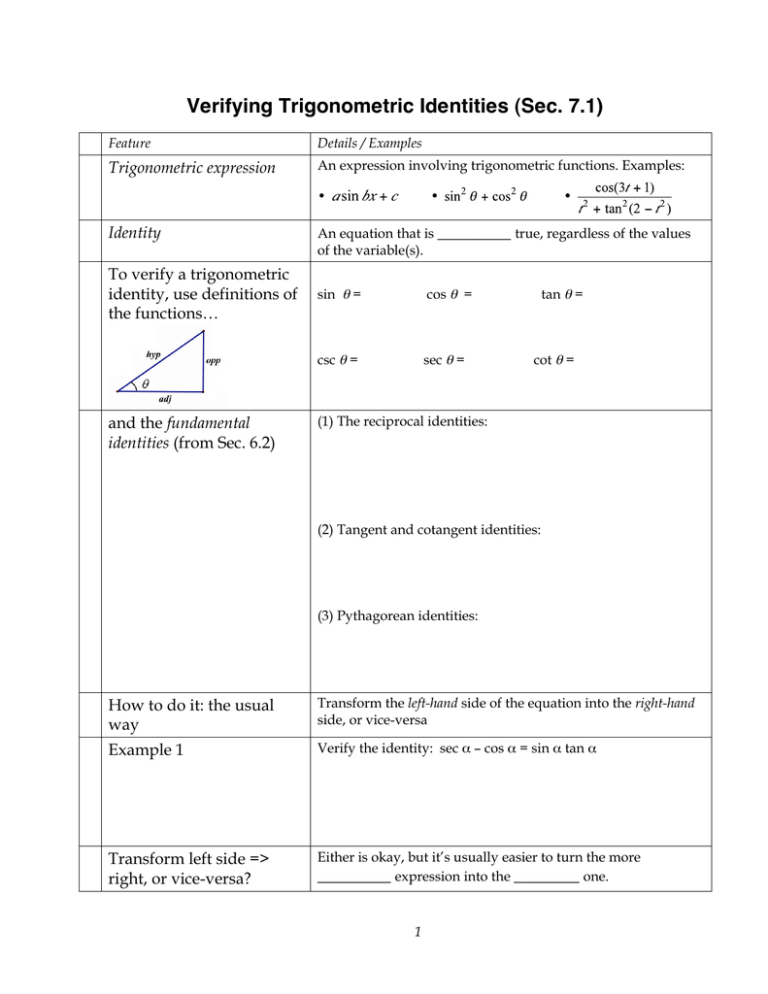



Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity
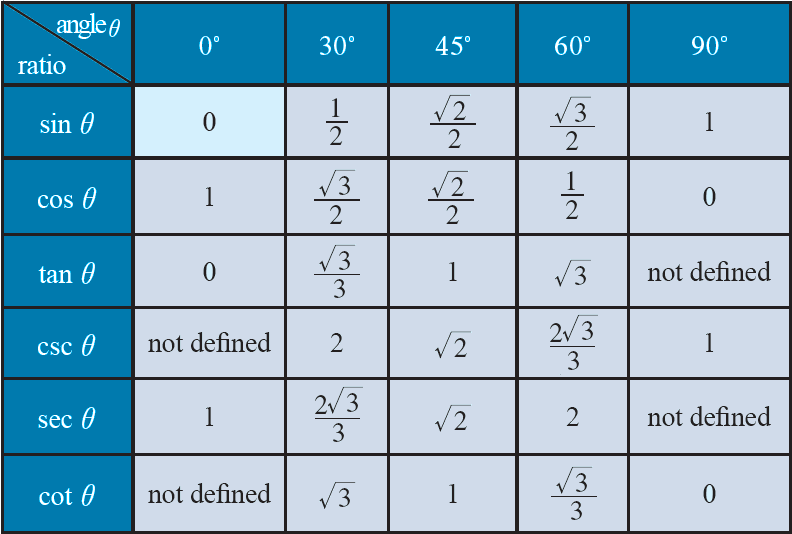



Trigonometric Identities




Art Of Problem Solving



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



1



A Trig Identity



Verifying Trigonometric Identities How To Do It The Easy Way Lesson Plan Spiral




Tangent Half Angle Formula Wikipedia




How To Use Double Angle Identities Studypug
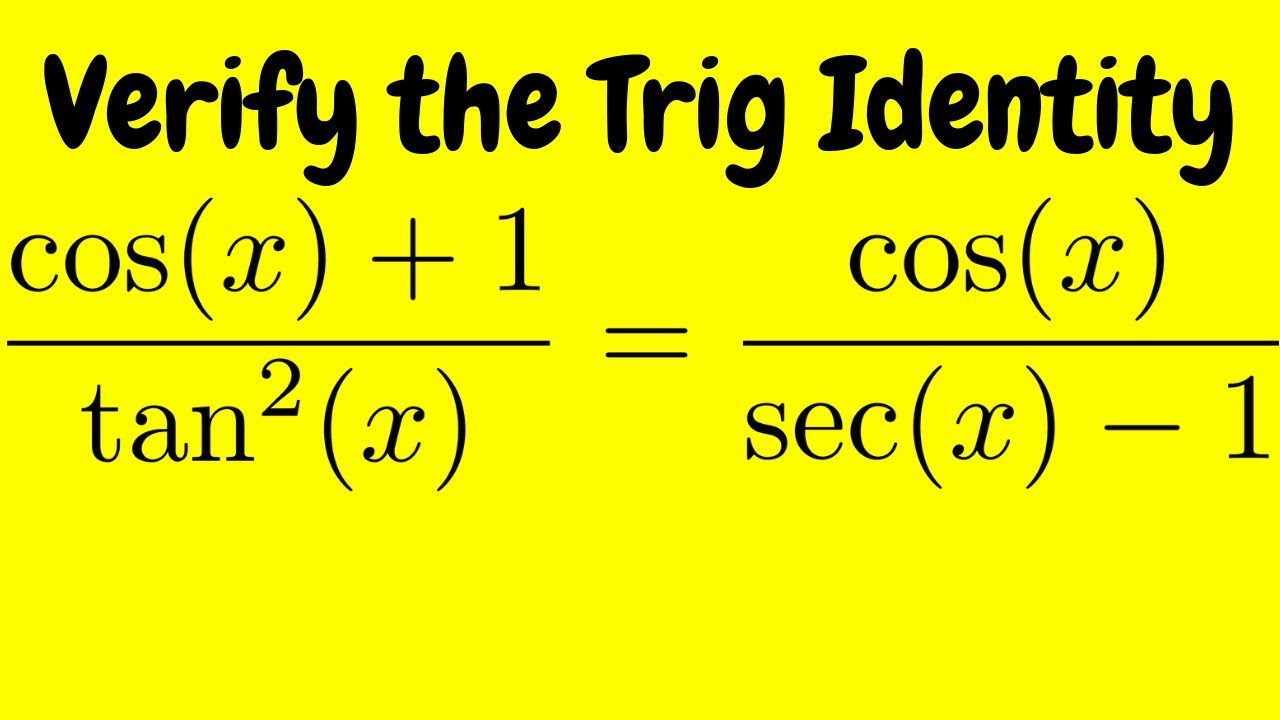



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube
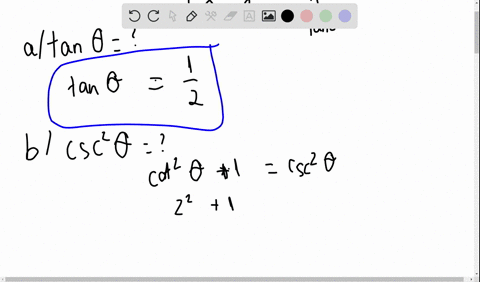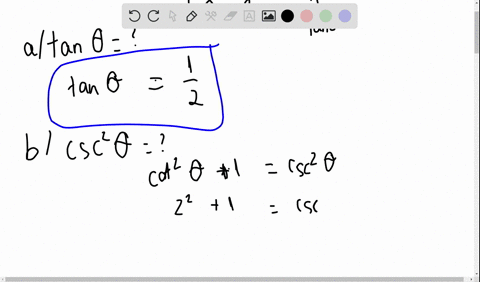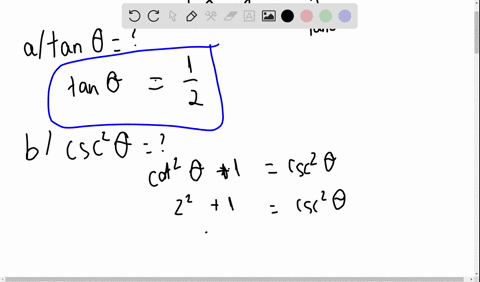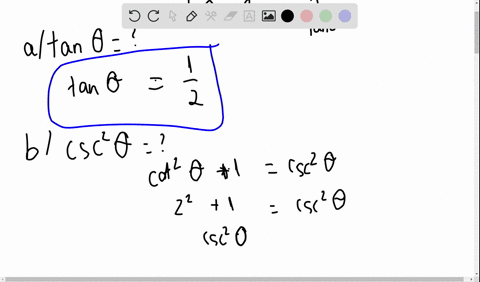



Solved Given Tan Theta 4 Use Trigonometric Identities To Find The Exact Value Of A Sec 2 Theta B Cot Theta C Cot Left Frac Pi 2 Theta Right D Csc 2 Theta




Trigonometric Identities Proofs List Of Trig Identities




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube
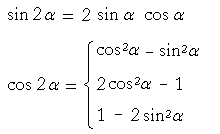



Trigonometric Identities Topics In Trigonometry



Ilectureonline




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Solved Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com




Use Trigonometric Identities To Solve Each Equation In The Interval 0 21 C X 2 Tan 2x Homeworklib




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




List Of Trigonometric Identities Wikipedia




Question Video Using The Pythagorean Identities To Evaluate A Trigonometric Function For An Angle Nagwa




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Trig Identities Bingo Card
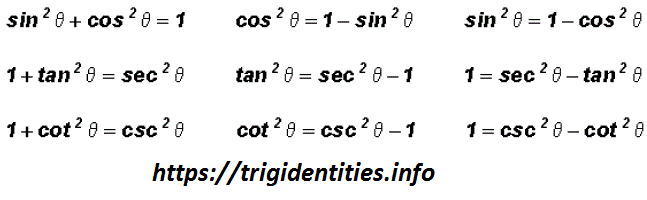



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities



2



Ilectureonline




Summary Of Trigonometric Identities
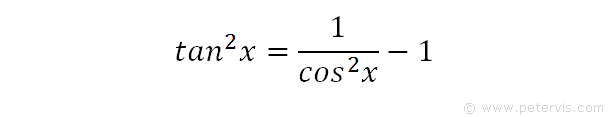



Integrate Tan 2x
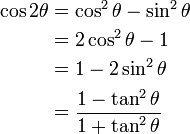



Trigonometric Identities




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions




Basic Trigonometric Identities And Equations Ppt Download



1




Trigonometric Identities A Plus Topper
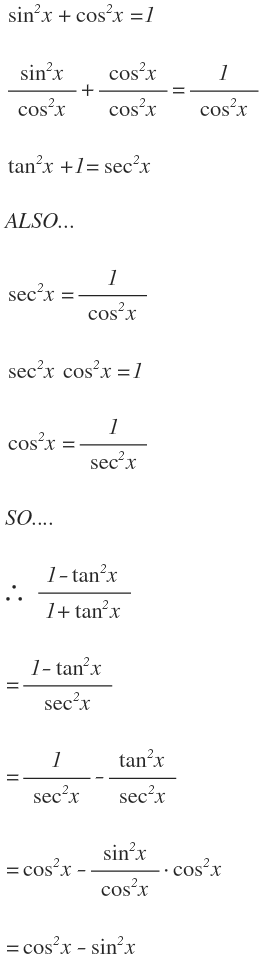



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Solved Does Tan 2 Theta Frac Sin 2 Theta Cos 2 Theta Justify Your Answer




Powers Of Trigonometric Functions




Solved Using Standard Trigonometric Identities Show That Chegg Com




Summary Of Trigonometric Identities




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube
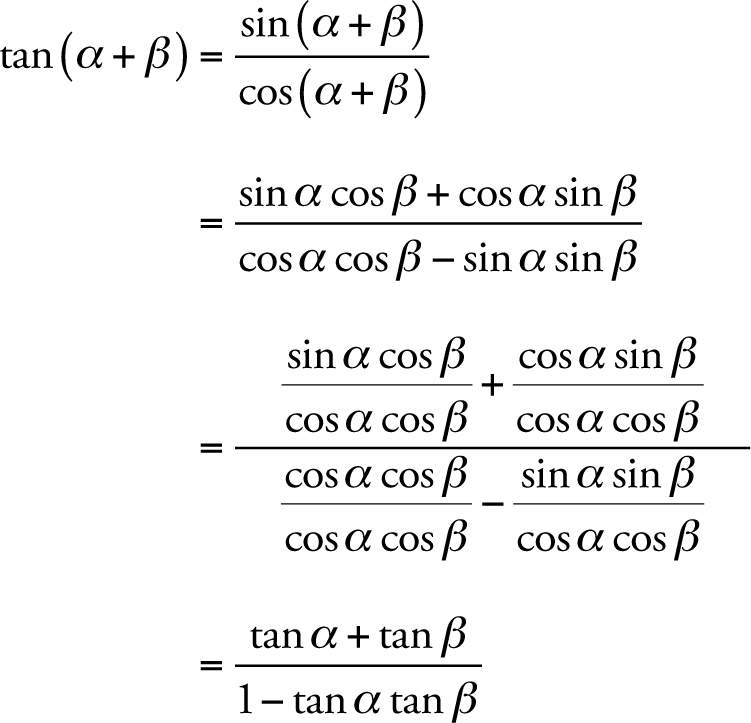



Tangent Identities




Ppt Analytic Trig Powerpoint Presentation Free Download Id




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic



Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero
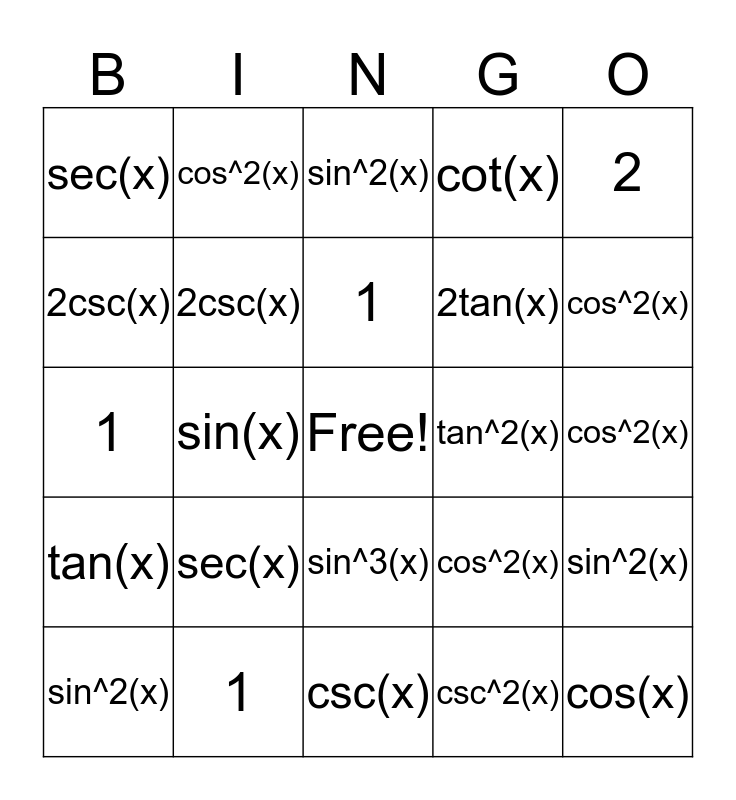



Trig Identities Bingo Card
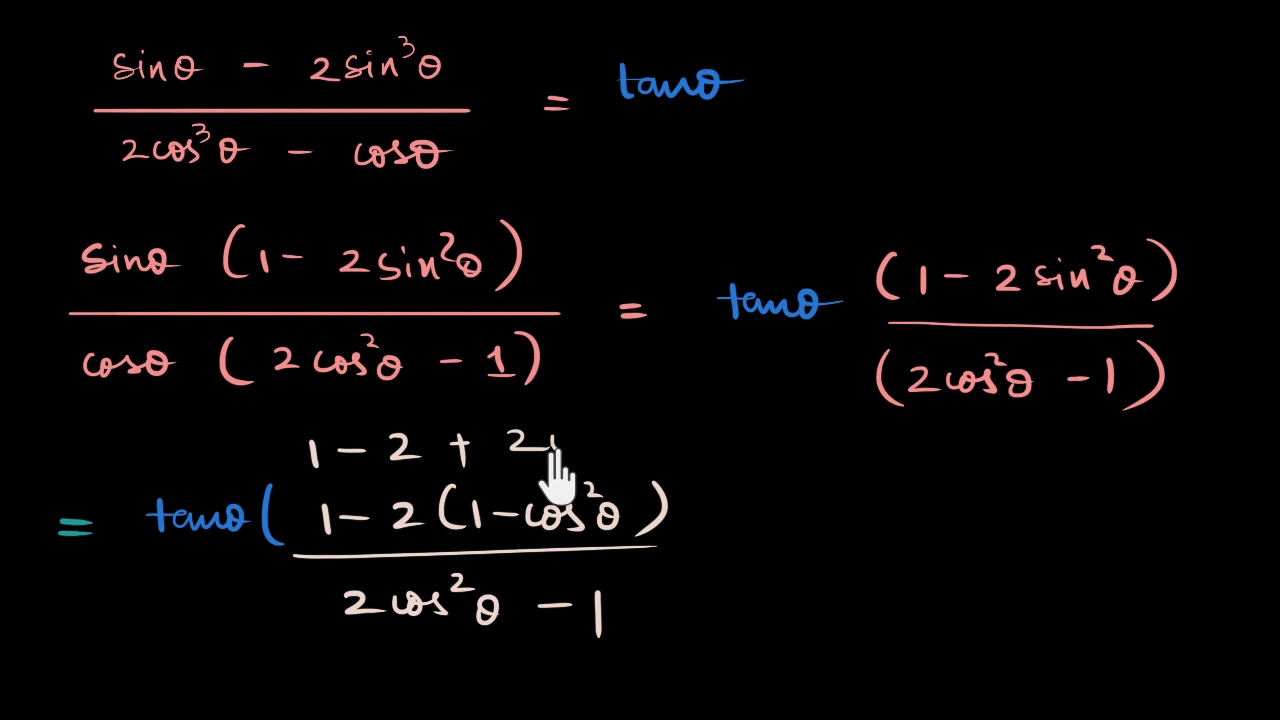



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy
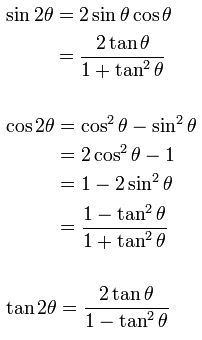



Trigonometric Identities Definition Rules Examples S Sigma Tricks



Sum To Product Formulas For The Tangent And The Cotangent Functions The Product To Sum Formulas For The Sine And Cosine Functions Trigonometric Identities Examples
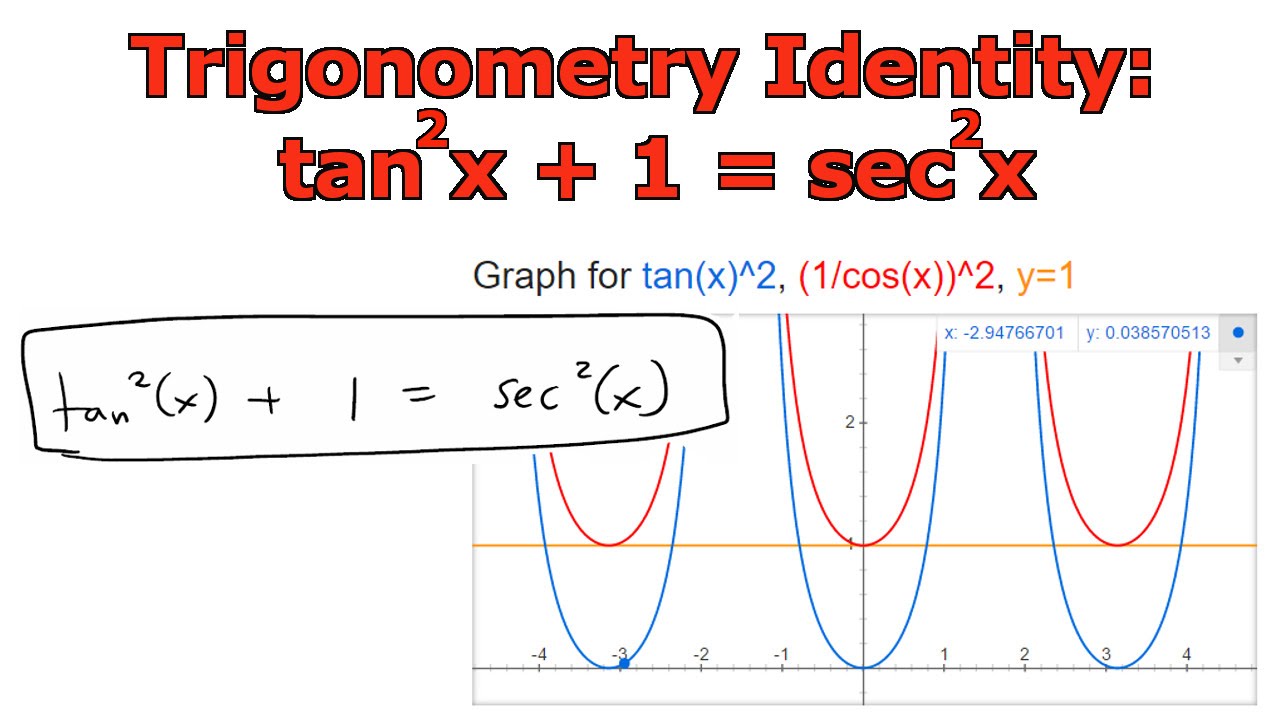



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Trig Identities Bingo Card




14 2 Trigonometric Identities



How I Remember Trig Identities Part 2 Beyond Solutions



Trigonometry Reciprocal Identities Expii




Summary Of Trigonometric Identities



The Trigonometric Ratios Of Angl



What Is The Formula Of Tan2x Quora




Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities
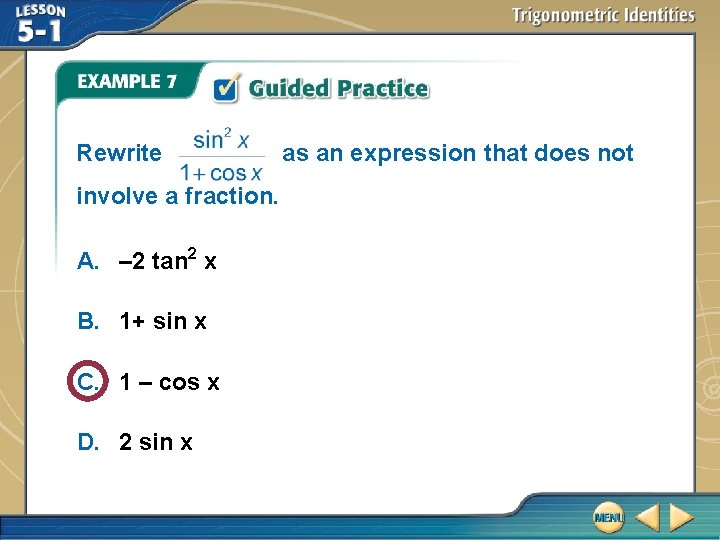



Lesson 5 1 Trigonometric Identities Fiveminute Check Over




Tangent Half Angle Formula Wikipedia




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube



Trigonometry Identities
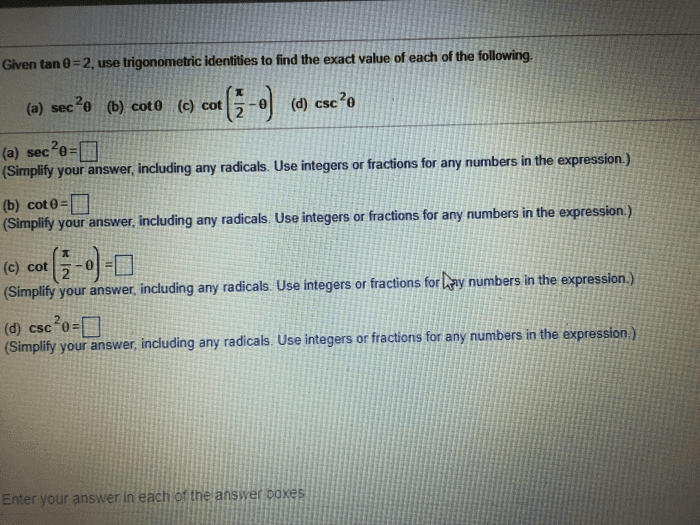



Oneclass Tan 0 2 Use Trigonometric Identities To Find The Exacd Value Of Each Of The Following A




7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig



2



Relating Trigonometric Functions Trigonometry Socratic



3
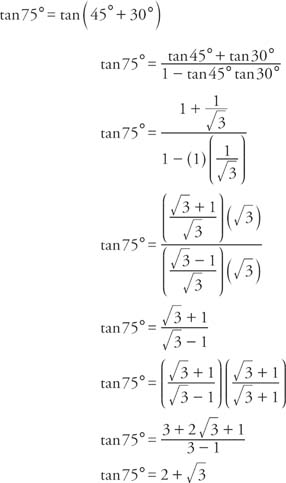



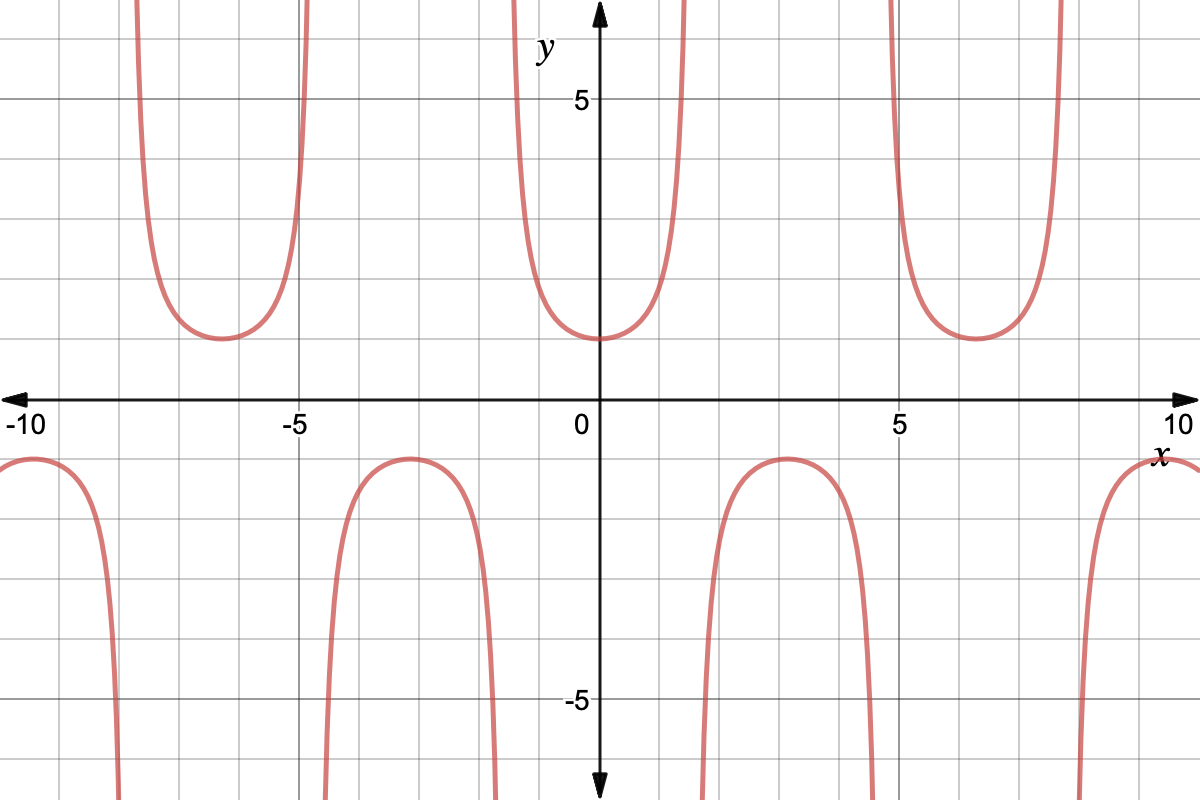
Tangent Identities




Solved Inquiry 11 8 Marks Prove The Following Trig Chegg Com
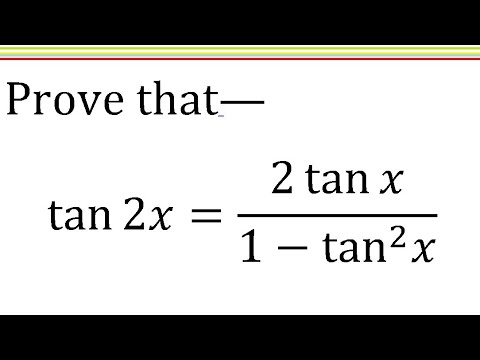



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




List Of Trigonometric Identities Wikipedia
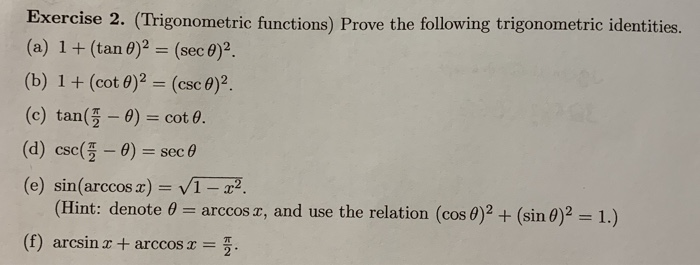



Solved Exercise 2 Trigonometric Functions Prove The Chegg Com




bestpictjcry Tan 2x Tan 2x




Powers Of Trigonometric Functions



7 Proving Ids Trig Functions Identities




Lesson 5 2 Verifying Trigonometric Identities By Griffin Heier




Tangent Identities



How To Solve Tan 2y Sec 2y Tan 4y Tan 2y Socratic




14 2 Trigonometric Identities




Worksheet On Trigonometric Identities Establishing Identities Hints




Trigonometric Identities List Of Trigonometric Identities Examples




Summary Of Trigonometric Identities
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



Trigonometric Identities
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com
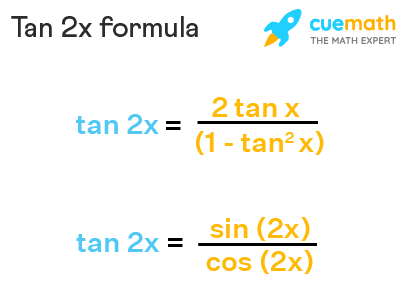



Tan 2x Formula What Is Tan 2x Formula Examples



0 件のコメント:
コメントを投稿